
On the XLMiner ribbon, from the Data Mining tab, select Predict - Multiple Linear Regression to open the Multiple Linear Regression - Step 1 of 2 dialog.Īt Output Variable, select MEDV, and from the Selected Variables list, select all remaining variables (except CAT. Select a cell on the Data_Partition worksheet. On the XLMiner ribbon, from the Data Mining tab, select Partition - Standard Partition to open the Standard Data Partition dialog. For more information on partitioning a data set, see the Data Mining Partition section. To partition the data into Training and Validation Sets, use the Standard Data Partition defaults with percentages of 60% of the data randomly allocated to the Training Set, and 40% of the data randomly allocated to the Validation Set. A portion of the data set is shown below. On the XLMiner ribbon, from the Applying Your Model tab, select Help - Examples, then Forecasting/Data Mining Examples to open the Boston_Housing.xlsx from the data sets folder.

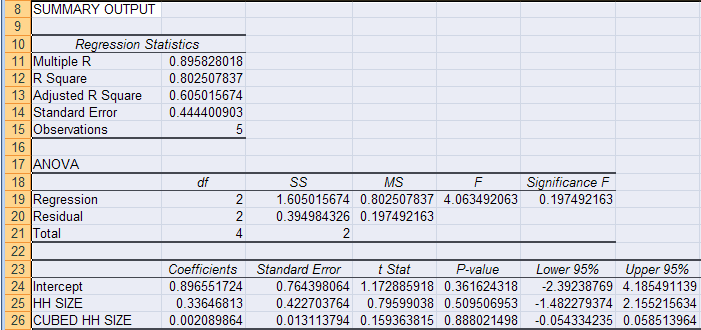
This variable will not be used in this example. MEDV, which has been created by categorizing median value (MEDV) into two categories: high (MEDV > 30) and low (MEDV < 30). In addition to these variables, the data set also contains an additional variable, Cat. A description of each variable is given in the following table. GROWTH: Given partial data about an exponential growth trend, fits an ideal exponential growth trend and/or predicts further values.The following example illustrates XLMiner's Multiple Linear Regression method using the Boston Housing data set to predict the median house prices in housing tracts. LOGEST: Given partial data about an exponential growth curve, calculates various parameters about the best fit ideal exponential growth curve. TREND: Given partial data about a linear trend, fits an ideal linear trend using the least squares method and/or predicts further values. The degrees of freedom, useful in looking up F statistic values in a reference table to estimate a confidence level, The F statistic, or F-observed value indicating whether the observed relationship between dependent and independent variables is random rather than linear,
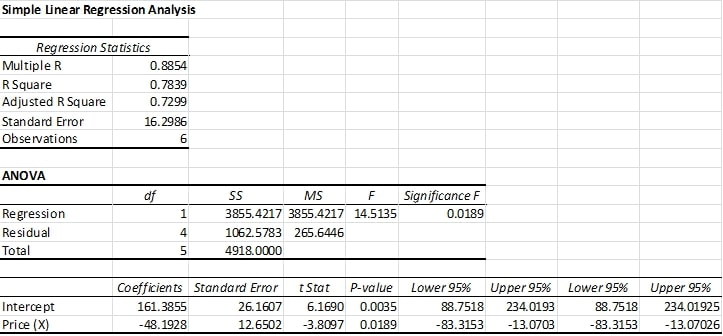
Standard error for the dependent variable values, The coefficient of determination (between 0 and 1, where 1 indicates perfect correlation), The standard error for each coefficient and the intercept, If verbose is TRUE, in addition to the set of linear coefficients for each independent variable and the y-intercept, LINEST returns Verbose - A flag specifying whether to return additional regression statistics or only the linear coefficients and the y-intercept (default). forces the curve fit to pass through the origin. Otherwise, forces b to be 0 and only calculates the m values if FALSE, i.e. if known_data_y is a single row, each row in known_data_x is interpreted as a separated independent value, and analogously if known_data_y is a single column.Ĭalculate_b - Given a linear form of y = m*x+b, calculates the y-intercept ( b) if TRUE. If known_data_y is a one-dimensional array or range, known_data_x may represent multiple independent variables in a two-dimensional array or range.
Known_data_x - The values of the independent variable(s) corresponding with known_data_y.
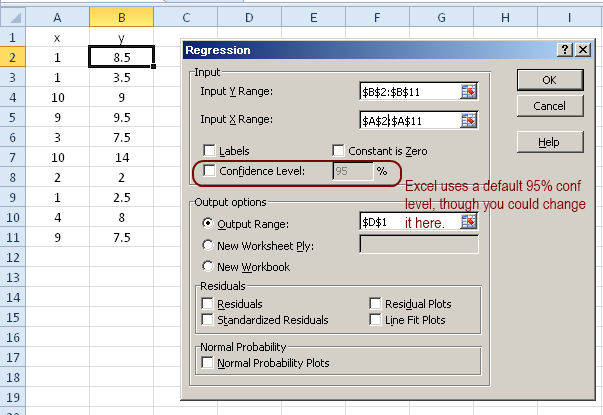
if known_data_y is a single row, each row in known_data_x is interpreted as a separated independent value, and analogously if known_data_y is a single column. If known_data_y is a one-dimensional array or range, known_data_x may represent multiple independent variables in a two-dimensional array or range. If known_data_y is a two-dimensional array or range, known_data_x must have the same dimensions or be omitted. Known_data_y - The array or range containing dependent (y) values that are already known, used to curve fit an ideal linear trend. LINEST(B2:B10, A2:A10, FALSE, TRUE) Syntax Given partial data about a linear trend, calculates various parameters about the ideal linear trend using the least-squares method.


 0 kommentar(er)
0 kommentar(er)
